This is my first post of a series of summaries of machine learning algorithms. I personally took this up to challenge myself to enhance my skill in communciating machine learning and statistical concepts to others. In this post, i would be talking about logistic regression which is still very widely used for classification in multiple industries.

Introduction
Logistic regression is primarily a binary classifier which is used when the dependent variable is a categorical variable. Although, we know that linear regression is used for a dependent continuous variable,it might be tempting to use linear regression for a classification task. But we should be aware of the fact that final prediction of linear regression can go beyond 1 and be less than 0 which are not acceptable as a probability value.
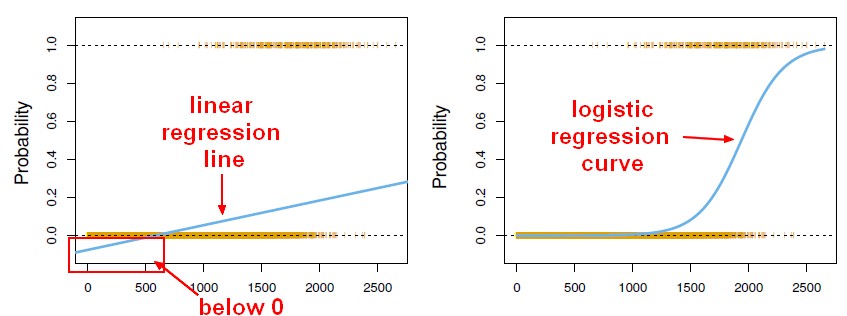
So this takes us to the next step of logistic regression which is the logit function.
Mathematical explanation
Following is a logit function in a matrix form with X being the independent variable matrix and Y being the probability value.
$${Pr}(Y=1/ {X}) = \frac{\text{e}^{\beta X}}{1 + \text{e}^{\beta X}}$$
``
It is also called sigmoid function.
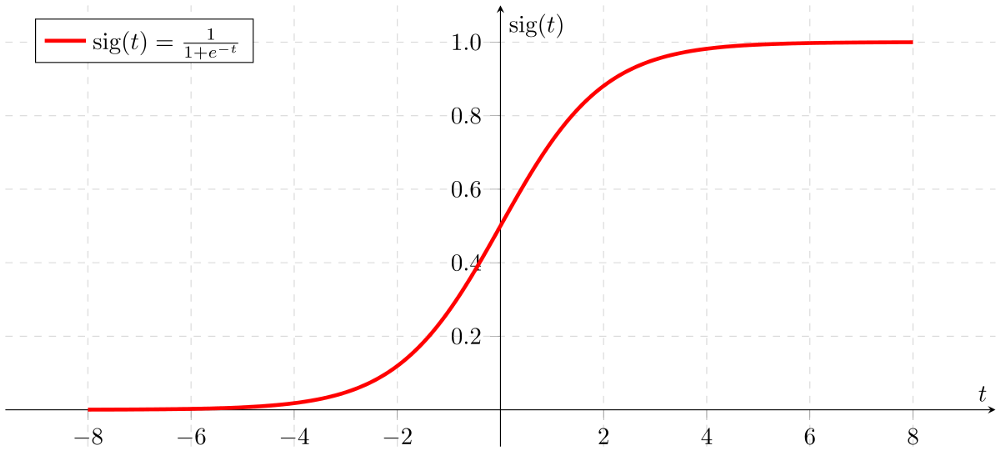
Logit function restricts the final prediction value between 0 and 1 and would help in making the final classfication by using a threshold value. Lets go ahead and understand how logistic regression works.
For simplicity, let us consider
$${Pr}({X}) = {Pr}(Y = 1/{X})$$
Now rearranging the logit equation we get, $$\frac{{Pr}({X})}{1 - {Pr}({X})} = \text{e}^{\beta X}$$
Now this will let us calculate the odds of a particular event happening and the value ranges from 0 to infinity. Taking log on both sides converts this into a linear equation which can be solved using maximum likelihood method. $$\ln (\frac{{Pr}({X})}{1 - {Pr}({X})}) = \beta X$$
In an situation with just one independent variable(x1), increasing the value of x1 changes the logodds by $\beta1$
Types of logistic regression:
1. Binary logistic regreesion: When there are only two putput classes
2. Multinomial : When there are more than 2 output classes
3. Ordinal : When the output classes are ordinal in nature like ratings(1 to 5)
How to do multiclass logistic regression using a binary logistic regression?
We will use all vs one approach to solve this problem.
Let’s say there are 4 classes in our dataset and 0,1,2,3 are their class labels
We will have to first train different logistic binary classifier in the following way.
1. We should fix one class as a reference class and will have to create 3 different binary classifiers one for each of the other classes.
2. Split the data into 3 parts, with each set containing the datapoints labelled with the selected 2 classes.
3. Build a classifier with classes 0 and 1 with 0 fixed as the reference class.
4. We will then obtain the parameter coefficient for the log odds of these 2 classes represented by the following equation.
5. In a similar fashion, we build 2 other logistic classifiers and estimate the respective beta coefficients($\ \beta_2 $,$\ \beta_3 $) for those classes.
Finally, it’s time to predict the class for a test data point.
Every single data point is passed through each of these 3 classifiers and log odds are calculated through classifiers.
There are 2 possible outcomes.
1. If any of the logodds are +ve and also the highest among the other classifiers, then we choose that class as the final label.
2. If all the log odds are -ve, then we choose the reference class, which is 0 in our case as the class label for the datapoint.
Keypoints in Logistic Regression:
- Does NOT assume a linear relationship between the dependent variable and the independent variables, but it does assume linear relationship between the logit of the explanatory variables and the response.
- Independent variables can be even the power terms or some other nonlinear transformations of the original independent variables
- The dependent variable does NOT need to be normally distributed, but it typically assumes a distribution from an exponential family (e.g. binomial, Poisson, multinomial, normal,…); binary logistic regression assume binomial distribution of the response
- The homogeneity of variance does NOT need to be satisfied
- Errors need to be independent but NOT normally distributed
- It uses maximum likelihood estimation (MLE) rather than ordinary least squares (OLS) to estimate the parameters, and thus relies on large-sample approximations
Implementation in R:
#### Creating train and test data
set.seed(99)
train <- createDataPartition(y=sel_features_dat_vf$y1,p=0.8,list=FALSE)
train_data <- sel_features_dat_vf[train,]
test_data <- sel_features_dat_vf[-train,]
set.seed(99)
model <- glm(train_data$y1 ~.,family=binomial(link='logit'),data=train_data)
summary(model)
#### Assessing the predictive ability of the model
fitted.results <- predict(model,test_data[,1:17],type='response')
answers = test_data$y1
# Confusion matrix
cm_logistic <- table(answers, fitted.results>= 0.3)
head(fitted.results)
# ROC Curve
ROCRpred <- prediction(fitted.results, test_data$y1)
ROCRperf_log <- performance(ROCRpred, 'tpr','fpr')
p_roc_logistic <- plot(ROCRperf_log, text.adj = c(-0.2,1.7))
#Sensitivity and specificity
sens_spec_ROCR <- performance(ROCRpred, measure = "sens",x.measure = "cutoff")
plot(sens_spec_ROCR, text.adj = c(-0.2,1.7))
# Calculating the cutoff
cost.perf = performance(ROCRpred, "cost")
ROCRpred@cutoffs[[1]][which.min(cost.perf@y.values[[1]])]
# AUC calculation
auc_ROCR <- performance(ROCRpred, measure = "auc")
auc_ROCR
References:
[1] https://newonlinecourses.science.psu.edu/stat504/node/164/
[2] https://towardsdatascience.com/logistic-regression-detailed-overview-46c4da4303bc
[3] https://www.theanalysisfactor.com/the-distribution-of-dependent-variables/